Урок за децибела: dB и dBm срещу печалба и миливат

Понятието за децибел (dB) е разбираемо трудно и объркващо за някой, който току-що се запознава с него. Комбинирането на спецификации за усилване, мощност и напрежение (и ток, но не толкова често), които смесват dB, dBm, dBW, ватове, миливата, напрежение, миливолта и т.н., често изисква преобразуване назад и напред между линейни стойности и децибелови стойности. Този кратък урок ще ви помогне да изясните разликата между работа с децибели и работа с линейни стойности.

Логаритмите (дневниците) са замислени за първи път в ранните 1600 от шотландския математик Джон Напиер, като инструмент за опростяване на операциите за умножение и деление, като ги преобразуват съответно в по-бързи и по-малко податливи на грешки операции на събиране и изваждане. Това става възможно поради начина, по който умножаването на две числа, изразени като сходни базови числа с експоненти, може да бъде постигнато чрез просто добавяне на експонентите заедно. Разделянето на същите тези числа се осъществява чрез изваждане на показателите. Това е един от законите на експонентите и изглежда така:

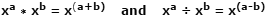
Използване на действителните числа като пример, където x = 10, a = 4, b = 1:

Законът на експонентите работи за всяко базово число, а не само за 10. На остроумие:

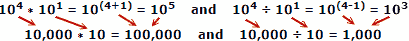
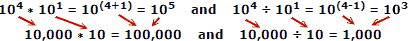
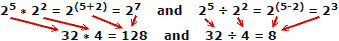
Хората са склонни да правят по-малко грешки при добавяне и изваждане на числа, така че предимството на логаритмите е очевидно. Не забравяйте, че логаритмите са разработени преди да са били налични автоматични механични или електронни компютри. Правилото за слайд използва свойствата на логаритмите за изчисляване, но това е отделна основна тема.

Това са прости примери, но имайте за основа или показател. При липса на калкулатор, за да бъдете полезни за общо приложение, се нуждаете от таблица с числа и техните еквивалентни логаритми. Таблиците с ранни журнали запълват обеми в зависимост от разстоянието между числата (1.000, 1.001, 1.002, 1.003, срещу 1.0, 1.1, 1.2, 1.3 и др.). Добрата новина за създателите на логаритъмни таблици е, че е необходимо само едно "десетилетие" от числа (например, 1 до 10), тъй като всяко предшестващо или разделящо се десетилетие е просто кратно на мощност на 10.

Забележка: В тази дискусия използвам база 10, тъй като това е основата на нашата обща система от числа - оттук и терминът „общ логаритъм“ за базови 10 логове. Може би сте чували за естествени логаритми, които използват основата на e, но e не се използва много често при изчисляване на скаларни електрическа мощност, напрежение и токови величини (въпреки че се използва, когато са включени фазови ъгли, т.е. идентичност на Ойлер). Естествените логаритми се пишат като ln (x) без 'e' индекс, докато обикновено базовите 10 логаритми се пишат просто като log (x) без 10 подпис; т.е. не loge (x) или log10 (x), съответно.

На база = 10 регистрационна таблица:

Полу-логаритмична 5 Cycles Engineering Graph Paper - RF CafeИзключението и специалният случай е logx (0) = Недефиниран. Това е така, защото няма сила, на която можете да повишите произволно число и да получите 0 (нула). Можете да асимптотизирате до нула, но не можете да стигнете до нула. Никога няма да бъде показано числото нула в лог скала; те обикновено работят от някаква мощност на 10 до друга мощност от десет. Пример за хартия с графичен журнал е показан вдясно. Той има „цикли“ или „десетилетия“ на обхвата на 5. Обърнете внимание, че на оста y няма нула.

Базовият 10 (общ) логаритъм на числото е показателят, на който 10 трябва да бъде повдигнат, за да получи това число. С други думи, тъй като 10, издигнат до силата на 2, е равен на 100 (102 = 100), дневникът на базовия 10 на 100 е 2 (log10 100 = 2).

Това е основният закон на логаритмите:


Извършване на същите умножения и деления като в горната част на страницата, като се използват действителни логаритми:



Това е добре, но в крайна сметка това е логаритъмът на числото, което търсите. Въпрос: С изключение на прост пример като този, как да получите нужния отговор? Отговор: Потърсете антилогарита (антилог) на резултата. В такъв случай:

Един по-строг и по-вероятен пример с числа, които не са цели числа на 10, може да изглежда нещо като следното:




 HP-35 калкулатор (уикипедия) - RF CafeКогато логаритъмът на 'x' е равен на 1.8444, антилогът е равен на 'x', което е 69.9



Използвах калкулатора си, за да търся журналите и антилозите за тези номера, но преди 1972, когато Hewlett Packard (HP) представи своя научен калкулатор HP-35, средният човек без достъп до корпоративен или университетски мейнфрейм компютър, необходим за използване на лог таблица за извършване на такива изчисления.

Кой си прави труда да използва логаритми днес, може да попитате? Много хора, включително и аз, доста често при изчисляване на каскадни параметри на системата като фигура на шума (NF) и точки на прехващане (IP). Простото събиране и изваждане на печалбите dB и мощност dBm стойности не работят с NF и IP. Управляващите формули използват умножение и деление на линейни стойности на усилване и мощност, което изисква първо да преобразуват dB и / или dBm в линейни числа (коефициент на усилване и mW), използвайки антилози, извършвайки каскадни изчисления и след това преобразувайки резултата обратно в dB и / или dBm с помощта на регистрационни файлове.

Не всички операции на системна каскада изискват преобразуване напред и назад. Например, ако е необходимо само общото усилване на системата и / или нивото на изходна мощност, тогава изчисленията могат да се извършват или с линейни единици (mW и множители), или с логаритмични единици (dBm и dB, съответно).

Определението на 'dB' и 'dBm'

Децибел (dB) в електротехниката се дефинира като 10 пъти по-голям от логаритма на база-10 на съотношение между две нива на мощност; напр. Pout / Pin (печалба, с други думи). На остроумие:

Следователно всички печалби, по-големи от 1, се изразяват като положителни децибели (> 0), а печалбите, по-малки от 1, се изразяват като отрицателни децибели (<0). Имайте предвид, че за случаите, в които повечето от нас се сблъскват, линейното съотношение на P1 / P2 трябва да бъде положително число (> 0), тъй като логаритъмът от 0 е недефиниран, а логаритъмът на отрицателните числа е сложен (те съдържат както реална, така и въображаема част) ). Стойността на dB обаче теоретично може да приеме всяка стойност между −∞ и + ∞, включително 0, което е печалба от 1 [10 * log (1) = 0 dB].

'dBm' е базирана на децибел единица мощност, която се отнася до 1 mW. Тъй като усилването на 0 dB е равно на усилване от 1, мощността на 1 mW е 0 dB по-голяма от 1 mW, или 0 dBm. По подобен начин мощност от dBW е децибел спрямо 1 W мощност.


Съответно, всички стойности на dBm по-големи от 0 са по-големи от 1 mW, а всички dBm стойности по-малки от 0 са по-малки от 1 mW (виж фиг. 1). Например, + 3.01 dBm е 3.01 dB по-голям от 1 mW; т.е. или 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). -3.01 dBm е 3.01 dB по-малко от 1 mW; т.е. или 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Следващата таблица дава някои числови примери, за да можете да видите връзката между mW и dBm. Същият набор от стойности, начертани в логаритмична скала, би създал права линия. Поради логаритмичната връзка графиката свързва по-малките стойности спрямо лявата вертикална ос. Увеличена версия на региона от 0 до 1 mW е въведена за по-голяма яснота.

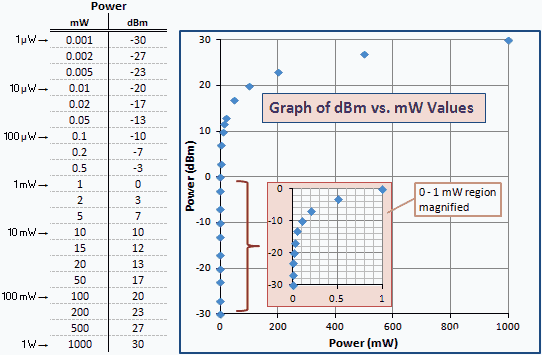
Фиг. 1 - Графика на мощността в единици на dBm спрямо mW

Фиг. 2 е таблица и графика на dB спрямо линейни коефициенти на усилване, подобни на dBm спрямо mW на фиг. 1. Обърнете внимание, че числата и кривите са абсолютно еднакви; само етикетите на осите се променят. Това е така, защото dBm е единица мощност, изразена в dB спрямо 1 mW (0 dBm).

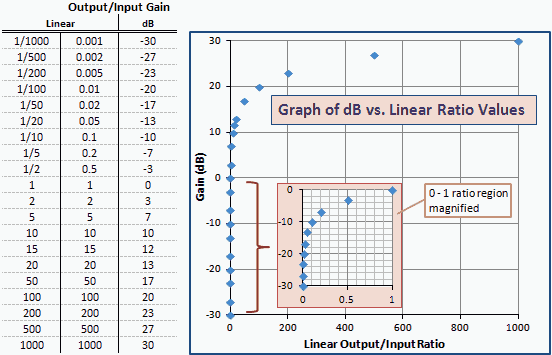
Фиг. 2 - Графика на печалбата в единици на dBm спрямо линейно съотношение

По принцип печалбата е множител (или деление) фактор. Като пример, един усилвател може да има усилване, което увеличава сигнала с фактор 4 (т.е. 4x) от вход към изход (вижте фиг. 3). Ако в усилвателя се подава сигнал 1 mW (0 dBm), тогава излиза 1 mW * 4 = 4 mW. По отношение на децибелите, коефициентът на 4 е еквивалентен на 10 * log (4) = 6.02 dB, така че 0 dBm плюс 6.02 dB на печалбата добива + 6.02 dBm на изхода.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

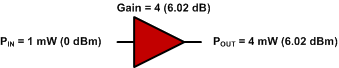
Фиг. 3 - Единично усилване на усилвателя.

Комбиниране на печалби (линейни и dB) w / положителна стойност

Ако усилвател с усилване на 4 е последователно с втори усилвател с усилване на 6, тогава общото усилване е 4 * 6 = 24. По отношение на децибелите, фактор на 6 е еквивалентен на 10 * log (6) = 7.78 dB, а коефициентът на 24 е еквивалентен на 10 * log (24) = 13.8 dB.

Точно както 4 x 6 = 24 (линейна печалба), 6.02 dB + 7.78 dB = 13.8 dB (децибел печалба).

Ако в усилвателя се подава 1 mW сигнал (0 dBm), тогава 4 mW излиза от първия усилвател, а 24 mW излиза от втория усилвател. Вижте фиг. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Фиг. 4 - Каскадно усилване на двоен усилвател.

Комбиниране на печалба и загуба (линейна и dB)
Този следващ пример показва какво се случва, когато се срещне печалба <1 (загуба), където атенюатор с печалба 1/6 се поставя след първия усилвател, вместо да има втори усилвател. Вижте фиг. 5.
4 * 1 / 6 = 2 / 3 (линейна печалба). По същия начин 6.02 dB - 7.78 dB = −1.76 dB (усилване на децибела).
Както при предишния пример, ако в усилвателя с усилване на 1 се подава 0 mW сигнал (4 dBm), тогава излиза 4 mW. След това 4 mW влиза в атенюатора с линейно усилване на 1 / 6 и излиза при ниво на мощност 4 / 6 mW (2 / 3 mW).
Общият коефициент на усилване в този случай е 4 / 6 = 2 / 3, така че изходната мощност всъщност ще бъде по-малка от входната мощност.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 стока

Фиг. 5 - Каскадно усилване на усилвателя и атенюатор.

12 mW + 34 mW + 8 mW + 20 dB

Допълнителна информация за логаритмите
Логаритми на продуктите
Свойството на логаритмите, използвани неявно по-горе, посочва следното и е в основата на възможността да се добавят и изваждат стойностите на логаритмите, вместо да се умножават техните линейни еквиваленти.

„h * j / k * m / n“ може да представлява каскада от компоненти, които имат три устройства (h, j и m), всяко с усилване> 1 и две устройства (k и n), всяко с усилване <1 (вж. Фиг. 6). Общото усилване на системата може да бъде изчислено или чрез умножаване на всички стойности на линейното усилване заедно, или добавяне на всички стойности на усилване в децибели.

Фиг. 6 - Каскадни компоненти

Логаритми на експонентите
Следното е важно за разбирането защо печалбата на мощност по отношение на мощността е 10 * log (Pout / Pin) dB, докато усилването на мощността по отношение на напрежението е 20 * log (Vout / Vin) dB.


което е така, защото cf е равно на c, умножено по себе си 'f' пъти. Например, ако f = 4:


Повишаване на мощността на базата на мощността срещу мощността на базата на напрежението
Повишаване на мощността е Pout / Pin, а усилването на напрежението е Vout / Vin. Повишение на мощността въз основа на съотношението на мощност в децибели се определя като 10 * log (Pout / Pin). Повишение на мощността по отношение на напрежението е [(Vout2 / R) / (Vin2 / R)], тъй като според закона на Ом P = V2 / R. 'R' в знаменателите отменя оставянето на Vout2 / Vin2, което е равно на (Vout / Vin) 2, както е дефинирано от правилото на експонентите, което казва ac ​​/ bc = (a / b) c. Следователно:

Важна забележка: Повишение на напрежението по отношение на напрежението е 10 * log (Vout / Vin) dB, същото като при усилването на мощността по отношение на мощността. Уравнението 20 * log (Vout / Vin) dB се прилага само когато усилването на мощността е изразено като напрежение. Това е често срещана точка на объркване.


Никоя операция в математиката не е произволна и това важи за това защо загубата на мощност на сигнала (печалба <1) се изобразява като отрицателна стойност и следователно се изважда по време на каскадно изчисление. Това е проста демонстрация, но достойна за споменаване.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Ако искате да изградите радиостанция, усилете вашия FM радиопредавател или се нуждаете от друг FM оборудване, моля не се колебайте да се свържете с нас: [имейл защитен].

Остави съобщение 

Списък на ЛС