Мощност и амплитуда: ватове, волта и реферирани децибели

Въведение
В радиочестотните приложения (но и в много други приложения) е много често да се работи с много големи и много малки сигнали. Например трансивърът може да предава мощност на 100 W и да получава само 10 fW (или 0.000'000'000'000'01 W). Тези изключително различни нива на мощност могат да споделят едни и същи вериги. Разбира се, тези цифри могат да бъдат изразени във ватове с помощта на инженерната нотация (както по-горе) или с научната нотация, като 1 · 102 W и 1 · 10 – 14 W, но те са доста трудни за произнасяне и ако експонентът е грешно написан , получената грешка ще бъде огромна.

Друг начин е да вземете логаритъма и да преобразувате всички сили в dBm. 100 W стават + 50 dBm, а 10 fW стават –110 dBm: тези цифри са много по-лесни за управление и писане. След това, ако затихването и усилването на различни блокове на веригата също се изразяват в dB, за да се намери крайната мощност, човек може просто да добави всичко заедно, вместо да умножава, като допълнително опростява изчисленията.

Не всички са удобни с dB, dBm и подобни (псевдо) единици: няма строга необходимост от използването им, но те са толкова широко използвани в инженерството, че е много трудно да се избегнат.

Някаква теория
Децибелите (dB) се използват за изразяване на съотношения на мощността по логаритмичен начин, така че много големи и много малки сили могат да се сравняват с помощта на удобни числа. Децибелът е безразмерна псевдо-единица, защото се определя от съотношението на две сили. Но тъй като децибелите са толкова удобни, за да се изрази истинска сила вместо просто безразмерно съотношение, много често се използват реферирани децибели.

Ако говорим за мощност, следното уравнение определя нивото на мощност P в dB на мощността p в W, отнасящо се до мощността p0:

Коефициентът 10 е, защото децибелите са "десети от камбаните". Но никога не съм чувал за каквото и да е измерване, направено в Bells, използват се само децибели.

Най-разпространената единица е dBm (произнася се "dBm"), известна също като dBmW или децибел-миливат: това е само нивото на мощност в dB в сравнение с референтната мощност на p0 = 1 mW. Понякога се използват и dBW и те изразяват съотношението на мощността спрямо p0 = 1 W, но те не са много чести.

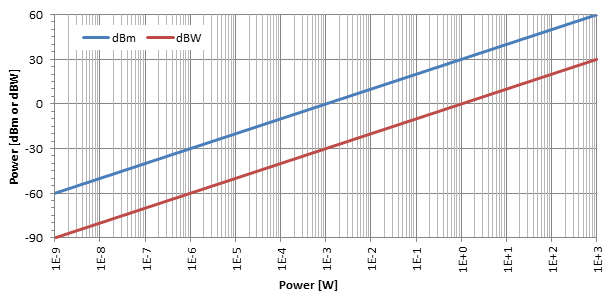
Както е показано на горния график, логаритмичният ефект от децибеловата конверсия е доста очевиден. Както може да се види на този график за регистрация, dBm и dBW са само две прави линии, разделени от 30 dB: за да конвертирате dBm в dBW, просто извадете 30.

В някои области, като например аналогов прием на телевизия, е обичайно да се измерва напрежението вместо мощност. Това не е проблем, стига импедансът да е известен и фиксиран (телевизионните приемници обикновено използват 75 Ω).

Абсолютните напрежения също могат да се възползват от децибеловата логаритмична скала, като използват децибел-микроволта (dBμV) и децибел-волта (dBV). Най-често срещаните са dBμV, които изразяват съотношението на напрежение спрямо u0 = 1 μV. Понякога се използват и dBV и те изразяват съотношението на напрежение спрямо u0 = 1 V.

Внимавайте, че напреженията използват "20" вместо "10" във тяхната dB формула. Това е така, защото децибелите винаги се определят като мощност; ако имаме само напрежения, първо трябва да ги квадратме, за да намерим силата. Тази сила на две, когато бъде извадена от логаритма, ще умножи съществуващия фактор на 10 по 2.

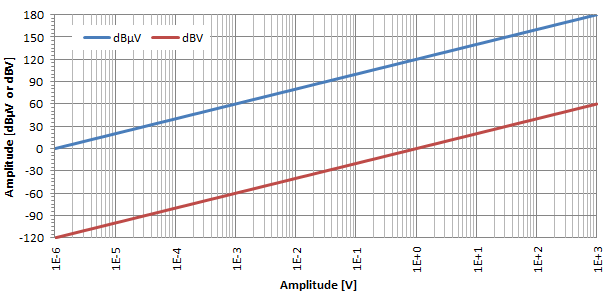
Както е показано на горния график и по подобен начин както преди, логаритмичният ефект от децибеловото преобразуване е доста очевиден и при напрежения. Както може да се види на този график, dBμV и dBV са само две прави линии, разделени от 120 dB: за да конвертирате dBμV в dBV, просто извадете 120.

Сега, ако искаме да преобразуваме от мощност в напрежение и обратно, трябва да знаем импеданса. Просто използваме следното уравнение:

Това преобразуване е валидно само когато импедансът Zc е реален и натоварването е съпоставено с електропровода.

Ако начертаем нивото на мощност в dBm и нивото на амплитудата в dBμV като функция на мощността в W за даден импеданс (тук Zc = 50 Ω), получаваме следното:

Както преди, имаме две успоредни линии 107 dB един от друг. Така че, за да преобразувате от dBm в dBμV, просто добавете 107 dB за Zc = 50 Ω, добавете 109 dB за Zc = 75 Ω, добавете 115 dB за Zc = 300 Ω или добавете 118 dB за Zc = 600 Ω.

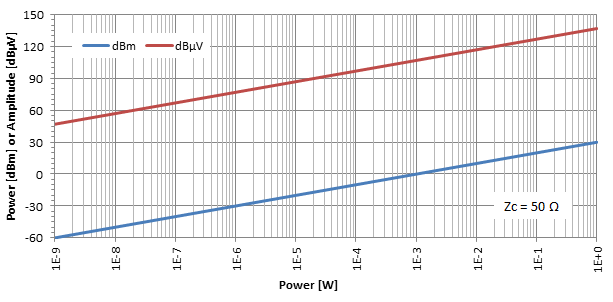
Практически съображения
На пръв поглед може да се мисли, че поради логаритъма, джобният калкулатор е абсолютно необходим за справяне с dBm. Всъщност грубото изчисление може лесно да се направи в главата ви. Трябва да запомните само три факта:
 Мощност на 1 mW е 0 dBm.
 Всеки път, когато мощността се удвои, добавете 3 dB.
 Всеки път, когато мощността се увеличава с коефициент 10, добавете 10 dB.

Сега, нека разгледаме няколко примера: да предположим, че имаме ниво на мощност от 26 dBm. Можем да напишем 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, и с предходните три правила за опростения можем лесно да намерим мощността, като правим 1 mW · 10 · 10 · 2 · 2 = 400 mW ,

Друг пример: да предположим, че имаме –33dBm: можем да запишем като –33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, и намираме 1 mW / 10 / 10 / 10 / 2 =.

Това работи и по обратния начин, например 50 mW са само 1 mW · 10 · 10 / 2. В dBm имаме 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Това изисква известна практика, но е много лесно да се направи. Не е толкова точен като джобния калкулатор, защото можете да бъдете точни само при ± 2 dB, но за усилието дава много добра представа за силата на сигнала.

Подобен метод работи и за dBμV, но правилата са различни:
 Амплитуда на 1 μV е 0 dBμV.
 Всеки път, когато амплитудата се удвои, добавете 6 dB.
 Всеки път, когато амплитудата се увеличава с коефициент 10, добавете 20 dB.

Може да се изненадате от изчисленията в децибели, показани преди, където dB се добавят към dBm, което е доста странно. Това е така, защото децибелите са псевдо единици и не се държат както обикновено. Съотношението на две сили се изразява в dB, но е безразмерно: например 3 dB означава само "два пъти повече". Мощността, изразена в dBm, наистина е мощност: например 10 dBm означава „10 пъти по-силна от 1 mW“, което е 10 mW.

Сега, когато добавите децибели (dB, dBm, ...), поради логаритмичната им природа, вие действително умножавате оригиналните цифри заедно. Така че, ако добавите печалба от 3 dB към мощност на 10 dBm, получавате 13 dBm. Но това, което наистина направихте, е умножаването на коефициент 2 с мощност на 10 mW, получаване на 20 mW, което е 13 dBm!

Засега добре, добавянето е много по-лесно да се направи в главата ви, отколкото да се умножавате, и това прави децибелите толкова удобни. Но има проблем: тъй като добавянето на децибели заедно съответства на умножаването на първоначалните фактори, как може да се добави (комбинира) силата на два сигнала? Е, не можеш. Не можете да добавите dBm към dBm. Ако например имате схема или устройство, което комбинира силата на един сигнал от 10 dBm (10 mW) с мощността на друг сигнал от 13 dBm (20 mW), резултатът е 10 mW + 20 mW = 30 mW, което е 14.8 dBm. Няма как да направите това директно в dBm, трябва да конвертирате и двете сили в Watts, да ги добавите заедно и да ги конвертирате обратно в dBm. Това е голямо ограничение на децибелите и обикновен провал; за щастие тази операция не е много честа.

Ако искате да изградите радиостанция, усилете вашия FM радиопредавател или се нуждаете от друг FM оборудване, моля не се колебайте да се свържете с нас: [имейл защитен].

Остави съобщение 

Списък на ЛС